让学生的思维有“广度”、“深度”
发布时间:2014-06-23
点击:
来源:本站原创
录入者:陈幼峰
让学生的思维有“广度”、“深度”
武进区洛阳中心小学 陈幼峰
思维品质是指个体在思维活动中智力特征的表现,也就是人与人之间的思维活动上表现的差异,它的品质包括思维的广阔性、思维的批判性、思维的深刻性、思维的灵活性和思维的敏捷性。这些方面是相互联系、密不可分的,是有机地统一在一起的。
在这刚参加工作的数年中,我发现现在有相当一部分学生的思维往往只停留在问题的表面或考虑问题不全面,当问题以另外一种形式出现时,往往会造成解题困难。下面我针对思维的广阔性、深刻性及其培养谈一点我的想法。
一、思维的广阔性及其培养
思维的广阔性,是指能全面而细致的考虑问题。它表现为思路开阔,能全面地分析问题,多方位、多角度地思考问题,善于对数学问题的特征、差异和隐含关系等进行具体分析,做出广泛的联想,能用各种不同的方法处理和解决问题,将它推广并应用于解决类似的问题上。善于运用各种形式的发散思维来思考问题是思维开阔的重要表现。具有广阔思维的人,不仅考虑问题的整体,还会考虑问题的细节;不但考虑问题的本质,而且考虑和问题有关的其他条件。教师要想培养学生思维广阔性可以从几个方面下手:
1、丰富学生数学知识
只有具备大量的数学知识,才能从事物的不同方面和不同联系上去考虑问题,从而避免片面性和狭隘性。如在教学时教师可以向学生多提供具有物体本质属性的变式,丰富学生的表象储备,有利于学生解决全面地思考问题。例如苏教版小学三年级数学上册中有这样一道应用题,“一共有42人去坐船,每只大船限乘4人,每条6元;每只小船限乘3人,每条5元,问你准备怎样租船?”虽然教材并没有让学生说出哪种方法最便宜,但我们作为数学教师却不能放过这样一个机会,我们应该先让学生自己讨论思考,说出他们的想法,然后教师可以用一一列举的方法,把每种可能性都列出来,让学生感受到其中的数学思想,开阔他们的眼界,使得你的学生见多识广。
2、一法多用
一种数学方法往往可以用来解决不同的问题,例如,除法验算既可以用来解决验算的问题,又可以解决( )÷( )= 6……5这一类求被除数的题目,像这样让学生通过联想,利用一个知识解决不同问题的方法,在进行复习时尤为有效,它不仅可以帮助学生整理知识,更重要的是可以开阔学生的思路,训练学生的思维。
研究题目,跳出思维定势。低年级的小学生很容易受思维定势的影响,如下面两道题目:
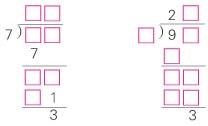
第一道思考题度并不是很大,但是学生由于学了两位数除以一位数的计算顺序,在思考时往往会按照平时的计算顺序去解答,这样就给解决这道问题带来了困难。这道题目的突破口在最下面几十一那里,多少乘7个位会出现1呢,显然只有3,然后再根据乘出来的结果依次推出其他地方的数字。第二题虽然突破口在开头,符合平时的计算顺序,可到了第二步就需要学生能展开联想,不能再按部就班。
3、培养发散式思维
发散式思维又叫求异思维,是沿着不同的方向去思考,对题目提供的信息重新加以组合,找出几种可能的答案。由于发散式思维本身就要求沿着不同的方向去思考,因此对于学生思维广阔性的培养有着直接的作用。但是教师在训练学生发散性思维时,要注意进行适当的引导,不可放任自流,虽然发散性思维强调用不同的方法思考,对于答案一时也很难确定是否正确,但是必须要做到每种方法都有据可依,并且教师对于每一种方法都要给予适当的评价。
二、思维的深刻性及其培养
思维的深刻性,是指能深入到事物的本质里面去考虑问题,善于钻研问题,能不被表面的现象所迷惑,能抓住问题的本质与核心。在认识事务时,若缺少对其本质深刻的揭示,其灵活性无从谈起、其批判性等将是无源之水、无本之木。《译林》(文摘版)曾刊登过这样一个笑话:“父:‘如果你有一个橘子,我再给你两个,那你数数看一共有几个橘子?’子:‘我不知道!在学校里,我们都是用苹果数数的。’”可能读者看了都会笑,因为根本不会有这样的老师和数学教学,我们在教学时不仅仅是给学生一些鲜明的例子,更重要的是我们帮助学生抽象出了数学的本质,所以没有发生这样的笑话。如何培养学生思维的深刻性,我认为可以从下面几点来着手:
1、从形象到抽象,为理论认识夯实基础
要培养学生思维的深刻性,首先要使学生的思维能逐步摆脱对直观材料的依赖,抽象概括出数学知识的本质和规律,而小学生的思维特点是从具体形象思维为主要形式逐步过渡到抽象逻辑思维为主要形式。因而,在教学过程中,教师应让学生自己动手摆一摆、做一做等直观的手段,让学生有个清晰地表象,从而为抽象出数学规律作好准备。
例如教学两位数除以一位数:“42除以2,怎样算?”时,先组织学生动手摆小棒,让学生先摆4捆和2根小棒,然后设问:把42根小棒平均分给2个班,怎么分呢?此时,教师引导学生先从4捆小棒里平均分给两个班,每班分到2捆,也就是20根,再把剩下的2根平均分给2个班,每班分到1根,合起来就是21根,这样进行教学就使学生对“把42根小棒平均分成2份怎样操作”有了鲜明的表象,紧接着让学生结合课本上的图下边竖式回想并复述操作过程,这样做不仅使学生弄清了笔算42÷2的算理,而且为下节课上升到理性认识打下了基础。
2、从现象到本质,培养判断能力
思维的深刻性不仅要求学生能认识事物的本质和规律,而且要能够不被表面现象所迷惑,抓住事物的本质与核心,作出正确的判断,这就要求学生具有一定的判断能力。学生能依据一定的数学规律,对所面临的数学问题做出恰当的判断,是培养思维深刻性的基本要求,因此,在教学中教师应经常组织学生运用所学概念对数学问题进行判断,并要求学生说明肯定或否定的理由,提高思维的自主性。
3、从旧知到新知,提高推理能力
概念、判断和推理是思维认识活动的基本形式。培养学生初步的逻辑推理能力历来是小学数学教学目的之一,也是思维具有深刻性所必须的,在数学教学中,我们既要注意传授新知识过程中培养学生的推理能力,又要注意在解题活动中培养学生的推理能力,提高学生思维的逻辑性。例如:在听一节其他老师上的数学课时,教师教授平行四边形面积时,让学生在复习旧知识的基础上,启发他们自己动手操作、动脑思考。学生用不同的方法把平行四边形拼成了长方形,并找到了两种图间的联系,最后用推理的方法找到了计算平行四边形的面积公式。
数学是思维的体操,数学教学不是简单地让学生掌握一些现成的数学知识,而是要在学生获取知识的过程中领会数学的思想和方法,训练学生的思维,提高学生的思维能力,最终帮助学生学会数学地思维。
附件:
|
|










