许多家长在闲聊时会跟我讲，有些数学题，我自己会做，但是却不会讲解。“只可意会，不可言传”是大多数人对于数学的理解，数学这门学科也因此有了一些高贵感、神秘感。其实，数学培养的是人的一种思维模式、思考方式，当我们把数学思维内化后，很多“为什么”已经成了“自然而然”，所以也就讲不出“因为所以”了。而教师的任务就是将“因为所以”分析清楚，把数学思维用一种可见的方式呈现出来。

线段图就是其中最直观的一种方式。

小学数学分数应用题是教学中的重点，也是难点。特别是分数乘除法的应用题，文字叙述比较抽象，数量关系比较复杂，小学生的思维又处于具体形象思维向抽象逻辑思维过渡的阶段，对一些复杂的应用题，如果用常规的思考方法难以获得解题途径时，可以采用画线段图的方法帮助分析，将思考的过程完全呈现出来，这样既可以帮助学生轻松、愉快的学习复杂关系的应用题，又能培养学生的能力、促进了思维的发展。

恰当使用线段图可使抽象问题具体化。

比如苏教版六年级上册分数连乘的实际问题：“六年级同学为国庆晚会做绸花。一班做了135朵，二班做的朵数是一班的，三班做的朵数是二班的。三班做了多少朵？”本题中有两个单位“1”的量，还有两个数量关系，线段图就可以完美地避开单位“1”混乱的情况。

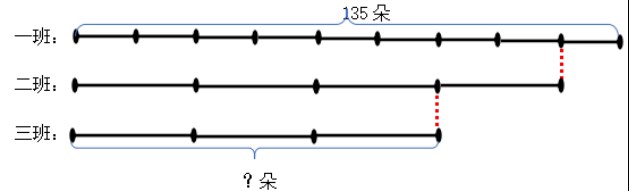
               ？朵

这道例题学生会出现列式“135××”，虽然计算结果与“135××”相同，但意义上却解释不了。出现这种错误，只要是因为学生不理解题意，不理解所写算式的意义。如果借助线段图帮助理解题意、分析数量关系，弄清楚每一步计算的什么，这种错误的算法就不会出现的。

巧妙使用线段图可使复杂问题简单化。

比如苏教版六年级上册数学书中的一道思考题：“小明和小红都养了一些金鱼，小明把自己金鱼条数的送给小红后，两人金鱼条数同样多。已知小明原来的金鱼比小红多8条，小红和小明原来各有金鱼多少条？”许多学生看到本题之后表示毫无头绪，只能看到条件当中有分率、有具体数量，但是这两者又不是相对应的。当我提示学生试着画线段图分析题意后，有半数渐渐有了思路。

从线段图中可以直观地看出8条金鱼对应的正是小明金鱼条数的，随后采用基本的分数应用题的解题方法（分率对应的量÷分率=单位“1”的量）就可以求出小明金鱼的条数，成功找到突破口。

巧妙地运用线段图，将出题者的数学思维一步一步呈现出来。当我们直观地观察简洁明了的线段图时，往往能一针见血地找到解题的关键。

数学语言往往是最精炼的、最简洁的，数学公式也会使用固定字母来表示一些数学名词，因此，在描述实际问题时，也有数学自己的一套——示意图，而线段图就是众多示意图中的一种。线段图能够简洁、直观地描述实际问题，肯定也能清晰地呈现人的数学思维。因此，当我们词不达意时、难以理解时，不妨试试画线段图，使抽象的问题具体化、复杂的问题简单化，直接将思考的过程呈现出来，比任何言语都有价值！